ความสัมพันธ์

ความสัมพันธ์
ความสัมพันธ์ อาจหมายถึง == ผูกพัน เกี่ยวข้อง
ความสัมพันธ์ทางสังคม ในสังคมศาสตร์ เป็นความสัมพันธ์ทางสังคมระหว่างบุคคลที่มากกว่าหนึ่งคนขึ้นไป
ความสัมพันธ์ระหว่างประเทศ เป็นกลยุทธ์ของแต่ละรัฐเพื่อรักษาผลประโยชน์ของชาติโดยนโยบายทางการต่างประเทศ      อ่านต่อ

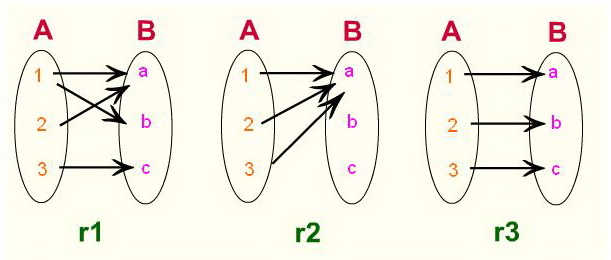
โดเมนและเรนจ์

โดเมนและเรนจ์
 พิจารณาเซตของสมาชิกตัวหน้า  และเซตของสมาชิกตัวหลังในคู่อันดับของความสัมพันธ์เช่น
 r  =  {(1,2),(2,4),(3,6),(4,8),(5,10)}
เซตของสมาชิกตัวหน้าในคู่อันดับของ  r  คือ  {1,2,3,4,5}  เรียกเซตของสมาชิกตัวหน้าในคู่อันดับของความสัมพันธ์  r  ว่า  โดเมน  ของ  r  เขียนแทนด้วย และเซตของสมาชิกตัวหลังในคู่อันดับของ  r  คือ  {2,4,6,8,10}  เรียกเซตของสมาชิกตัวหลังในคู่อันดับของความสัมพันธ์  r  ว่า เรนจ์ ของ  r  เขียนแทนด้วย         อ่านเพิ่มเติม

ความสัมพันธ์และฟังก์ชัน

ความสัมพันธ์และฟังก์ชัน
คู่อันดับ (Order Pair) เป็นการจับคู่สิ่งของโดยถือลำดับเป็นสำคัญ เช่น คู่อันดับ a, b จะเขียนแทนด้วย (a, b) เรียก a ว่าเป็นสมาชิกตัวหน้า และเรียก b ว่าเป็นสมาชิกตัวหลัง(การเท่ากับของคู่อันดับ) (a, b) = (c, d) ก็ต่อเมื่อ a = c และ b = dผลคูณคาร์ทีเชียน (Cartesian Product) ผลคูณคาร์ทีเซียนของเซต A และเซต B คือ เซตของคู่อันดับ (a, b) ทั้งหมด โดยที่ a เป็นสมาชิกของเซต A และ b เป็นสมาชิกของเซต B         อ่านต่อ

การนําสมบัติของจํานวนจริงไปใช้ในการแก้สมการกําลังสอง

การนําสมบัติของจํานวนจริงไปใช้ในการแก้สมการกําลังสอง
การนำสมบัติของจำนวนจริงไปใช้ในการแก้สมการกำลังสองตัวแปร : อักษรภาษาอังกฤษตัวเล็ก เช่น x , y ที่ใช้เป็นสัญลักษณ์แทนจำนวนค่าคงตัว : ตัวเลขที่แททนจำนวน เช่น 1, 2นิพจน์ : ข้อความในรูปสัญลักษณื เช่น 2, 3x ,x-8 ,เอกนาม : นิพจน์ที่เขียนอยู่ในรูปการคูณของค่าคงตัวแปรตั้งแต่หนึ่งตัวขึ้นไปที่มีเลขชี้กำลังของตัวแปรเป็นจำนวนเต็มบวกหรือศูนย์ เช่น -3, 5xy , 2yพหุนาม : นิพจน์ที่สามารถเขียนในรูปของเอกนาม หรือการบวกเอกนามตั้งแต่สองเอก นามขึ้นไป เช่น 3x , 5x +15xy+10x+5      อ่านต่อ

สมบัติของจํานวนจริงเกี่ยวกับการบวกและการคูณ

สมบัติของจํานวนจริงเกี่ยวกับการบวกและการคูณ
จำนวนจริง
จำนวนตรรกยะ (rational number) เป็นจำนวนจริงที่สามารถเขียนได้ในรูปเศษส่วนของจำนวนเต็มที่ตัวส่วนไม่เป็นศูนย์ และเขียนในรูปทศนิยมซ้ำได้
จำนวนอตรรกยะ (irrational number) เป็นจำนวนจริงที่ไม่ใช่จำนวนตรรกยะซึ่งไม่สามารถเขียนในรูปทศนิยมซ้ำหรือเศษส่วนของจำนวนเต็มที่ตัวส่วนไม่เป็นศูนย์แต่เขียนได้ในรูปทศนิยมไม่ซ้ำ และ
สามารถกำหนดค่าโดยประมาณได้    อ่านต่อ

จำนวนจริง

จำนวนจริง
จำนวนจริง คือจำนวนที่สามารถจับคู่หนึ่งต่อหนึ่งกับจุดบนเส้นตรงที่มีความยาวไม่สิ้นสุด (เส้นจำนวน) ได้ คำว่า จำนวนจริง นั้นบัญญัติขึ้นเพื่อแยกเซตนี้ออกจากจำนวนจินตภาพ จำนวนจริงเป็นศูนย์กลางการศึกษาในสาขาคณิตวิเคราะห์จำนวนจริง (real analysis)
มีหลักเกณฑ์ในการแบ่งจำนวนจริงอยู่หลายเกณฑ์ เช่น จำนวนตรรกยะ หรือ จำนวนอตรรกยะ; จำนวนพีชคณิต (algebraic number) หรือ จำนวนอดิศัย; และ จำนวนบวก จำนวนลบ หรือ ศูนย์    อ่านต่อ

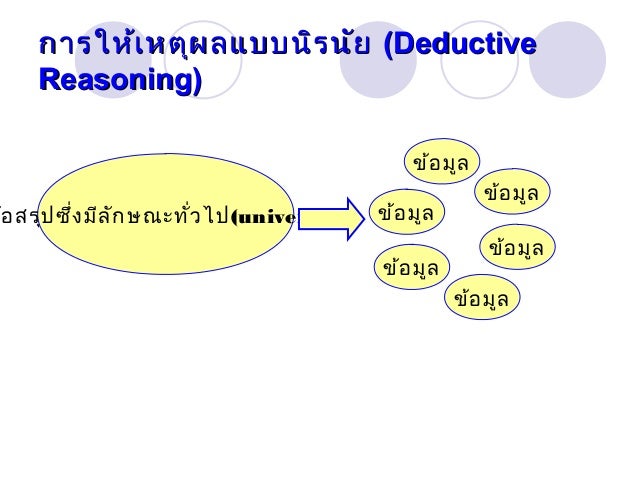
การให้เหตุผลแบบนิรนัย

การให้เหตุผลแบบนิรนัย
การให้เหตุผลแบบนิรนัยเป็นการนำความรู้พื้นฐานซึ่งอาจเป็นความเชื่อ ข้อตกลง กฎ หรือบทนิยาม ซึ่งเป็นสิ่งที่รู้มาก่อน และยอมรับว่าเป็นความจริงเพื่อหาเหตุผลนำไปสู่ข้อสรุป เป็นการอ้างเหตุผลที่มีข้อสรุปตามเนื้อหาสาระที่อยู่ภายในขอบเขตของข้ออ้างที่กำหนด
  ตัวอย่างที่ 1      เหตุ   1.สัตว์เลี้ยงทุกตัวเป็นสัตว์ไม่ดุร้าย

                                                     2. แมวทุกตัวเป็นสัตว์เลี้ยง

                                            ผล     แมวทุกตัวเป็นสัตว์ไม่ดุร้าย          อ่านต่อ